Как построить уравнение регрессии в Excel: пошаговая инструкция и советы

В этой статье мы рассмотрим, как построить уравнение регрессии в Excel, используя встроенные инструменты программы. Регрессионный анализ — это мощный статистический метод, который позволяет выявить зависимость между переменными и использовать её для прогнозирования или анализа данных. Мы разберём, как правильно подготовить данные, выбрать тип регрессии (линейная или нелинейная), а также как интерпретировать полученные результаты.

Вы узнаете, как использовать функцию "Регрессия" в инструменте "Анализ данных", а также познакомитесь с другими полезными функциями, такими как LINEST и FORECAST, которые помогут рассчитать коэффициенты и сделать прогнозы. Кроме того, мы обсудим, как избежать распространённых ошибок, таких как недостаточная подготовка данных или неправильный выбор типа регрессии.

Регрессионный анализ в Excel может быть полезен для прогнозирования, анализа взаимосвязей между переменными и оптимизации процессов. Мы также затронем тему улучшения точности модели с помощью методов, таких как метод наименьших квадратов, и рассмотрим, как интерпретировать статистические критерии для оценки качества модели.

Подготовка данных для регрессионного анализа

Подготовка данных — это первый и один из самых важных этапов построения уравнения регрессии в Excel. На этом этапе необходимо убедиться, что данные достаточно качественные и подходят для анализа. Для начала соберите все необходимые данные в таблицу Excel. Убедитесь, что каждая переменная находится в отдельном столбце, а каждая строка представляет собой отдельное наблюдение. Отсутствие пропущенных значений и корректный формат данных — ключевые моменты, которые следует учитывать. Если в данных есть выбросы или аномалии, их стоит обработать, так как они могут исказить результаты анализа.

После сбора данных важно провести предварительный анализ. Это включает в себя проверку на линейную зависимость между переменными, если вы планируете использовать линейную регрессию. Для этого можно построить диаграмму рассеяния, чтобы визуально оценить, существует ли связь между независимой и зависимой переменными. Если связь нелинейная, возможно, потребуется выбрать другой тип регрессии или преобразовать данные. Также стоит проверить данные на мультиколлинеарность, если вы работаете с несколькими независимыми переменными, так как это может повлиять на точность модели.

Наконец, перед началом анализа убедитесь, что данные нормализованы или стандартизированы, если это необходимо. Это особенно важно, если переменные имеют разные единицы измерения или масштабы. Правильная подготовка данных не только упростит процесс построения модели, но и повысит её точность и надежность.

Выбор типа регрессии: линейная или нелинейная

При построении уравнения регрессии в Excel первым шагом является определение типа зависимости между переменными. Линейная регрессия предполагает, что связь между независимой и зависимой переменными можно описать прямой линией. Этот метод подходит, если данные демонстрируют устойчивую линейную тенденцию. Однако в реальных задачах часто встречаются более сложные зависимости, которые требуют использования нелинейной регрессии.

Нелинейная регрессия применяется, когда связь между переменными лучше описывается кривой, например, экспоненциальной, логарифмической или полиномиальной. Важно понимать, что выбор типа регрессии зависит от характера данных и цели анализа. Например, если вы работаете с данными, которые растут или убывают с ускорением, линейная модель может оказаться недостаточно точной.

Для определения подходящего типа регрессии рекомендуется визуализировать данные с помощью диаграмм рассеяния. Это позволит оценить характер зависимости и принять обоснованное решение. Также стоит учитывать, что неправильный выбор модели может привести к некорректным результатам и ошибочным прогнозам. Поэтому перед началом анализа важно тщательно изучить данные и выбрать наиболее подходящий метод.

Использование инструмента Регрессия в Excel

Регрессионный анализ — это мощный статистический инструмент, который позволяет выявить зависимость между переменными и построить математическую модель для прогнозирования. В Excel для этого используется встроенный инструмент Регрессия, доступный через Анализ данных. Этот инструмент автоматически рассчитывает коэффициенты уравнения регрессии, предоставляет статистическую информацию о модели и помогает оценить её точность.

Чтобы начать работу, необходимо убедиться, что данные подготовлены корректно. Зависимая переменная (то, что вы хотите предсказать) и независимые переменные (факторы, влияющие на зависимую переменную) должны быть организованы в столбцы. После этого можно перейти к Анализу данных в меню Данные, выбрать инструмент Регрессия и указать диапазоны данных.

Важно правильно настроить параметры анализа, такие как уровень значимости и вывод остатков. После выполнения анализа Excel предоставит таблицу с результатами, включая коэффициенты уравнения регрессии, R-квадрат (показатель качества модели) и статистическую значимость переменных. Интерпретация этих данных поможет понять, насколько хорошо модель описывает зависимость и можно ли её использовать для прогнозирования.

Использование инструмента Регрессия в Excel требует внимательности, особенно при выборе типа модели (линейная или нелинейная) и проверке допущений, таких как нормальность распределения остатков. Однако при правильном подходе этот инструмент становится незаменимым помощником для анализа данных и принятия решений.

Интерпретация результатов регрессионного анализа

После построения уравнения регрессии в Excel важно правильно интерпретировать полученные результаты. Коэффициенты регрессии показывают, насколько сильно каждая независимая переменная влияет на зависимую. Например, если коэффициент положительный, это означает, что увеличение значения переменной приводит к росту результата, и наоборот. Коэффициент детерминации (R²) является ключевым показателем, который отражает, насколько хорошо модель объясняет вариацию данных. Чем ближе значение R² к 1, тем точнее модель описывает зависимость между переменными.

Однако важно помнить, что высокая точность модели не всегда свидетельствует о её применимости. Статистическая значимость коэффициентов проверяется с помощью p-значения. Если p-значение меньше 0,05, это говорит о том, что переменная оказывает значимое влияние на результат. Также стоит обратить внимание на остатки модели — разницу между фактическими и предсказанными значениями. Их анализ помогает выявить возможные ошибки в модели, такие как неучтённые факторы или нелинейные зависимости.

Для более глубокого понимания результатов можно использовать доверительные интервалы, которые показывают диапазон возможных значений коэффициентов. Это помогает оценить надёжность модели и её применимость для прогнозирования. В заключение, интерпретация результатов регрессионного анализа требует не только внимательного изучения числовых показателей, но и понимания контекста данных, чтобы избежать ошибочных выводов.

Оптимизация модели для повышения точности

После построения уравнения регрессии важно убедиться, что модель достаточно точна и адекватно описывает данные. Оптимизация модели позволяет улучшить её качество и повысить достоверность прогнозов. Для этого необходимо провести анализ остатков, проверить выполнение основных предположений регрессионного анализа, таких как линейность, гомоскедастичность и нормальность распределения ошибок. Если эти условия не выполняются, модель может давать некорректные результаты.

Одним из ключевых методов оптимизации является исключение незначимых переменных. Если в модели присутствуют переменные, которые не оказывают существенного влияния на зависимую переменную, их удаление может улучшить точность модели. Для оценки значимости переменных используются t-статистики и p-значения, которые можно получить с помощью инструмента Регрессия в Excel. Также полезно проверить модель на мультиколлинеарность, так как высокая корреляция между независимыми переменными может исказить результаты.

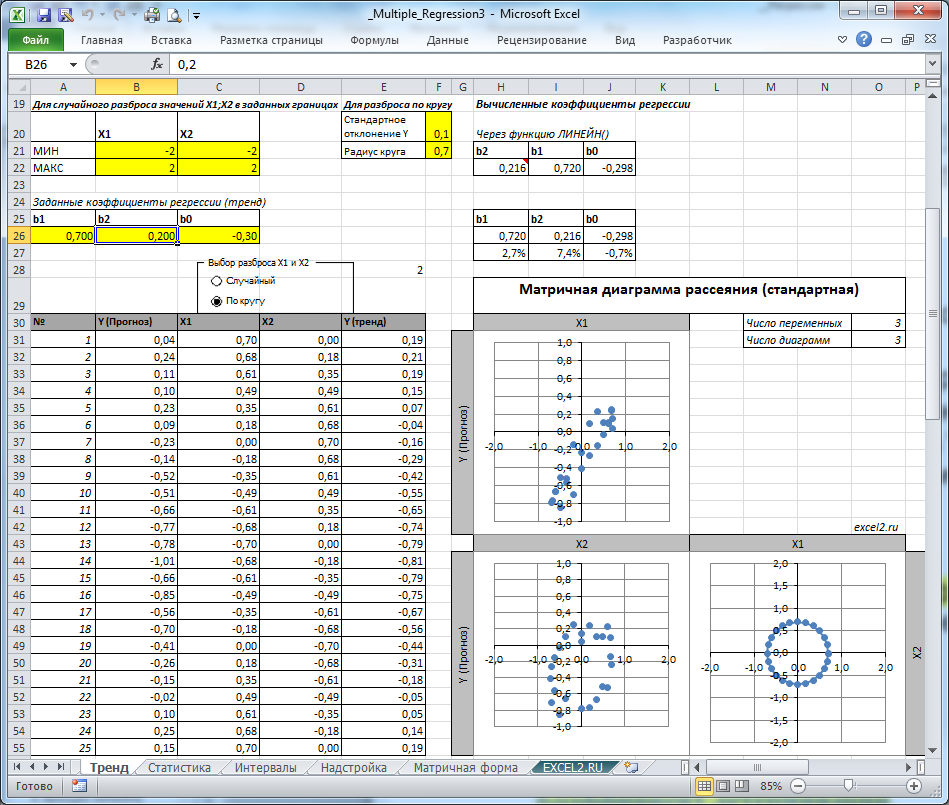
Для повышения точности модели можно использовать метод наименьших квадратов, который минимизирует сумму квадратов отклонений между наблюдаемыми и предсказанными значениями. В Excel это реализовано через функцию ЛИНЕЙН, которая автоматически рассчитывает коэффициенты регрессии. Дополнительно можно применить кросс-валидацию, разделив данные на обучающую и тестовую выборки, чтобы оценить, насколько хорошо модель работает на новых данных. Эти шаги помогут сделать модель более надёжной и пригодной для практического использования.

Заключение

Регрессионный анализ — это мощный инструмент для анализа данных, который позволяет выявить зависимости между переменными и строить прогнозы. В Excel этот процесс становится доступным даже для пользователей без глубоких знаний в статистике благодаря встроенным функциям и инструментам. Основные шаги включают подготовку данных, выбор типа регрессии (линейной или нелинейной), настройку параметров и интерпретацию результатов. Важно помнить, что качество модели зависит от корректности входных данных и правильного выбора метода анализа.

Использование функций LINEST и FORECAST позволяет не только рассчитать коэффициенты уравнения, но и сделать прогнозы на основе полученной модели. Однако для повышения точности модели стоит учитывать такие аспекты, как оптимизация параметров и проверка статистической значимости результатов. Регрессионный анализ в Excel открывает широкие возможности для анализа данных, прогнозирования и оптимизации процессов, что делает его незаменимым инструментом в работе с большими объемами информации.

Часто задаваемые вопросы

1. Как подготовить данные для построения уравнения регрессии в Excel?

Перед построением уравнения регрессии важно правильно подготовить данные. Убедитесь, что ваши данные организованы в таблице, где каждая строка представляет отдельное наблюдение, а столбцы — переменные. Зависимая переменная (то, что вы хотите предсказать) должна быть в одном столбце, а независимые переменные (факторы, влияющие на зависимую переменную) — в других. Убедитесь, что данные не содержат пропусков или ошибок, так как это может исказить результаты анализа. Также рекомендуется проверить данные на наличие выбросов, которые могут негативно повлиять на точность модели.

2. Какие инструменты Excel использовать для построения уравнения регрессии?

Для построения уравнения регрессии в Excel можно использовать встроенные инструменты анализа данных. Для этого необходимо активировать надстройку "Анализ данных" через меню "Файл" → "Параметры" → "Надстройки". После активации выберите инструмент "Регрессия" в разделе "Анализ данных". В открывшемся окне укажите диапазон для зависимой и независимых переменных, а также выберите параметры вывода результатов. Excel автоматически рассчитает коэффициенты уравнения регрессии и предоставит статистическую информацию, такую как R-квадрат и p-значения.

3. Как интерпретировать результаты регрессионного анализа в Excel?

После выполнения регрессионного анализа Excel предоставляет таблицу с результатами. Коэффициенты уравнения регрессии показывают, как каждая независимая переменная влияет на зависимую. Например, положительный коэффициент указывает на прямую зависимость, а отрицательный — на обратную. R-квадрат (коэффициент детерминации) показывает, насколько хорошо модель объясняет вариацию данных: значение ближе к 1 указывает на высокую точность модели. P-значения помогают определить статистическую значимость переменных: если p-значение меньше 0,05, переменная считается значимой.

4. Какие советы помогут улучшить точность регрессионной модели в Excel?

Для повышения точности регрессионной модели важно учитывать несколько факторов. Во-первых, убедитесь, что данные нормализованы или стандартизированы, особенно если переменные имеют разные масштабы. Во-вторых, проверьте данные на мультиколлинеарность (сильную корреляцию между независимыми переменными), так как это может исказить результаты. Используйте диаграммы рассеяния для визуальной оценки взаимосвязей между переменными. Также рассмотрите возможность добавления полиномиальных членов или взаимодействий между переменными, если это улучшает модель. Наконец, всегда проверяйте остатки модели на нормальность и отсутствие систематических ошибок.