Регрессионный анализ в Excel: шаги, функции и интерпретация результатов

Регрессионный анализ — это статистический метод, который позволяет исследовать взаимосвязи между переменными и строить модели для прогнозирования. В этой статье мы рассмотрим, как проводить регрессионный анализ в Excel, начиная с подготовки данных и заканчивая интерпретацией результатов. Вы узнаете, как использовать встроенные функции, такие как LINEST и LOGEST, для построения линейных и нелинейных моделей, а также как анализировать коэффициенты и графики для принятия обоснованных решений.

Мы обсудим основные этапы работы: от выбора зависимых и независимых переменных до проверки данных на корректность. Особое внимание уделим интерпретации результатов, включая анализ коэффициента корреляции и построение уравнений регрессии. Эти знания помогут вам не только понять, как работают модели, но и применять их для оптимизации процессов и прогнозирования в различных областях.

Основные понятия регрессионного анализа

Регрессионный анализ — это статистический метод, который позволяет изучать зависимости между переменными и строить модели для прогнозирования значений. В основе этого метода лежит идея о том, что одна переменная (называемая зависимой) может быть выражена через одну или несколько других переменных (называемых независимыми). Например, можно исследовать, как уровень продаж зависит от затрат на рекламу или как успеваемость студентов связана с количеством часов, потраченных на подготовку.

Одним из ключевых понятий в регрессионном анализе является коэффициент корреляции, который показывает силу и направление связи между переменными. Этот коэффициент может принимать значения от -1 до 1, где 1 указывает на сильную прямую связь, -1 — на сильную обратную, а 0 — на отсутствие связи. Однако корреляция не всегда означает причинно-следственную связь, поэтому важно интерпретировать результаты с осторожностью.

Регрессионный анализ может быть линейным или нелинейным в зависимости от характера зависимости между переменными. В линейной регрессии предполагается, что связь между переменными можно описать прямой линией, тогда как в нелинейной регрессии используются более сложные функции, такие как квадратичные или экспоненциальные. Кроме того, в случае, когда на зависимую переменную влияет несколько факторов, применяется многофакторная регрессия, которая учитывает взаимодействие между независимыми переменными.

Типы регрессионного анализа: линейная, нелинейная и многофакторная

Регрессионный анализ — это статистический метод, который позволяет исследовать взаимосвязи между переменными. В зависимости от характера этих взаимосвязей выделяют несколько типов регрессионного анализа. Линейная регрессия является наиболее простым и распространённым типом, где зависимость между переменными описывается прямой линией. Она подходит для случаев, когда связь между независимой и зависимой переменной можно выразить линейным уравнением. Этот метод часто используется для прогнозирования и анализа трендов.

Нелинейная регрессия применяется, когда связь между переменными имеет более сложный характер и не может быть описана прямой линией. В этом случае используются криволинейные модели, такие как полиномиальные, экспоненциальные или логарифмические функции. Нелинейная регрессия позволяет учитывать более сложные зависимости, что делает её полезной в задачах, где линейные модели оказываются недостаточно точными.

Многофакторная регрессия используется, когда на зависимую переменную влияет несколько независимых факторов. Этот тип анализа позволяет учитывать сложные взаимодействия между переменными и строить модели, которые более точно отражают реальные процессы. Многофакторная регрессия особенно полезна в экономике, биологии и других областях, где на результат влияет множество факторов. Каждый из этих типов регрессии имеет свои особенности и применяется в зависимости от характера данных и целей исследования.

Подготовка данных и их нормализация

Подготовка данных — это первый и один из самых важных этапов регрессионного анализа. На этом этапе необходимо убедиться, что данные корректны, полны и готовы для дальнейшего анализа. Нормализация данных играет ключевую роль, особенно если переменные имеют разные масштабы или единицы измерения. Это позволяет избежать искажения результатов из-за различий в диапазонах значений. Например, если одна переменная измеряется в тысячах, а другая — в единицах, это может привести к некорректной интерпретации коэффициентов регрессии.

Перед началом анализа важно проверить данные на наличие пропущенных значений и выбросов. Пропущенные значения могут исказить результаты, а выбросы — значительно повлиять на коэффициенты регрессии. Для обработки пропущенных значений можно использовать методы замены на среднее значение или медиану, а для выбросов — методы их исключения или преобразования. Также рекомендуется провести визуальный анализ данных с помощью диаграмм рассеяния, чтобы выявить возможные аномалии или нелинейные зависимости.

Нормализация данных может включать стандартизацию или масштабирование переменных. Стандартизация предполагает приведение данных к среднему значению, равному нулю, и стандартному отклонению, равному единице. Это особенно полезно, если данные имеют разные единицы измерения. Масштабирование, в свою очередь, позволяет привести значения к определенному диапазону, например, от 0 до 1. Эти шаги помогают улучшить точность и интерпретируемость результатов регрессионного анализа.

Использование функций Excel: LINEST и LOGEST

Функции LINEST и LOGEST в Excel являются ключевыми инструментами для проведения регрессионного анализа. Они позволяют не только строить модели, но и получать статистические данные, необходимые для оценки качества регрессии. LINEST используется для линейной регрессии, где зависимая переменная линейно связана с одной или несколькими независимыми переменными. Эта функция возвращает массив значений, включая коэффициенты уравнения регрессии, стандартные ошибки и коэффициент детерминации (R²), который показывает, насколько хорошо модель объясняет вариацию данных.

LOGEST, в свою очередь, применяется для экспоненциальной регрессии, где зависимость между переменными описывается экспоненциальной функцией. Эта функция также возвращает массив данных, включая коэффициенты уравнения и статистические показатели. Обе функции требуют аккуратного ввода данных и понимания их структуры, так как они работают с массивами. Важно помнить, что результаты, возвращаемые этими функциями, требуют дополнительной интерпретации, особенно в части проверки статистической значимости коэффициентов.

Использование LINEST и LOGEST значительно упрощает процесс анализа, но требует внимательного подхода к подготовке данных. Например, перед применением этих функций рекомендуется проверить данные на наличие выбросов и нормализовать их, если это необходимо. Кроме того, важно учитывать, что эти функции не предоставляют визуализацию результатов, поэтому для наглядности стоит дополнительно построить графики, чтобы лучше понять характер зависимости между переменными.

Интерпретация результатов: анализ коэффициентов и графиков

После проведения регрессионного анализа в Excel важно правильно интерпретировать полученные результаты, чтобы сделать обоснованные выводы. Коэффициенты регрессии играют ключевую роль в понимании влияния независимых переменных на зависимую. Каждый коэффициент показывает, насколько изменится зависимая переменная при изменении соответствующей независимой переменной на единицу, при условии, что остальные переменные остаются неизменными. Например, положительный коэффициент указывает на прямую зависимость, а отрицательный — на обратную.

Уравнение регрессии позволяет прогнозировать значения зависимой переменной на основе известных значений независимых переменных. Например, в случае линейной регрессии уравнение имеет вид y = a + bx, где y — зависимая переменная, x — независимая переменная, a — свободный член, а b — коэффициент наклона. Это уравнение можно использовать для построения прогнозов и анализа сценариев.

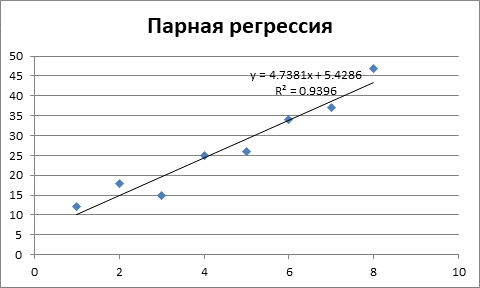
Графики являются важным инструментом визуализации результатов регрессионного анализа. Линия тренда на графике помогает оценить, насколько хорошо модель описывает данные. Если точки данных близки к линии тренда, это свидетельствует о высокой точности модели. Также полезно анализировать остатки — разницу между фактическими и предсказанными значениями. Их равномерное распределение вокруг нуля указывает на отсутствие систематических ошибок в модели.

Интерпретация результатов также включает оценку коэффициента детерминации (R²), который показывает, какая доля изменчивости зависимой переменной объясняется моделью. Чем ближе значение R² к 1, тем лучше модель описывает данные. Однако важно помнить, что высокий R² не всегда означает, что модель идеальна, особенно если в данных присутствуют выбросы или мультиколлинеарность.

Заключение

Регрессионный анализ в Excel — это мощный инструмент, который позволяет исследовать взаимосвязи между переменными и делать прогнозы на основе данных. В процессе анализа важно учитывать, что зависимая переменная (то, что мы хотим предсказать) и независимые переменные (факторы, влияющие на результат) должны быть корректно подготовлены. Это включает проверку данных на наличие выбросов, нормализацию и устранение пропущенных значений. Только после этого можно приступать к построению модели.

Использование функций Excel, таких как LINEST для линейной регрессии или LOGEST для экспоненциальной, значительно упрощает процесс анализа. Эти функции позволяют не только получить уравнение регрессии, но и оценить его точность через коэффициент детерминации (R²). Интерпретация результатов включает анализ коэффициентов уравнения, которые показывают, насколько сильно каждая независимая переменная влияет на зависимую.

Важно помнить, что регрессионный анализ — это не только математический инструмент, но и способ принятия обоснованных решений. Графическое представление данных, например, диаграммы рассеяния с линией тренда, помогает визуализировать взаимосвязи и сделать выводы более наглядными. Однако, при интерпретации результатов следует учитывать ограничения модели, такие как мультиколлинеарность или нелинейность зависимостей, которые могут исказить выводы.

В заключение, регрессионный анализ в Excel — это доступный и эффективный метод для анализа данных, который помогает выявить скрытые закономерности и улучшить качество прогнозов. Однако успех анализа зависит от корректности подготовки данных, выбора подходящего типа регрессии и грамотной интерпретации результатов.

Часто задаваемые вопросы

1. Как выполнить регрессионный анализ в Excel?

Для выполнения регрессионного анализа в Excel необходимо сначала убедиться, что у вас установлен Пакет анализа данных. Если он не установлен, перейдите в Файл → Параметры → Надстройки → Пакет анализа и активируйте его. Затем вставьте свои данные в таблицу, выберите Данные → Анализ данных → Регрессия. Укажите диапазон входных данных для зависимой и независимой переменных, выберите параметры вывода и нажмите ОК. Excel автоматически рассчитает коэффициенты регрессии, стандартные ошибки и другие статистические показатели.

2. Какие функции Excel используются для регрессионного анализа?

Для регрессионного анализа в Excel можно использовать как встроенные функции, так и инструменты из Пакета анализа данных. Основные функции включают ЛИНЕЙН(), которая возвращает статистику для линейной регрессии, и ТЕНДЕНЦИЯ(), которая предсказывает значения на основе линейного тренда. Также полезны функции КОРРЕЛ() для расчета коэффициента корреляции и СТОШYX() для оценки стандартной ошибки прогноза. Однако для более глубокого анализа рекомендуется использовать Пакет анализа данных, так как он предоставляет более полную информацию.

3. Как интерпретировать результаты регрессионного анализа в Excel?

Результаты регрессионного анализа в Excel включают несколько ключевых показателей. Коэффициенты регрессии показывают, насколько сильно каждая независимая переменная влияет на зависимую. R-квадрат указывает на долю объясненной дисперсии — чем ближе значение к 1, тем лучше модель описывает данные. P-значение помогает определить статистическую значимость коэффициентов: если оно меньше 0,05, переменная считается значимой. Также важно обратить внимание на стандартные ошибки и доверительные интервалы, которые показывают точность оценок.

4. Какие ограничения имеет регрессионный анализ в Excel?

Хотя Excel удобен для выполнения регрессионного анализа, он имеет ряд ограничений. Во-первых, он не поддерживает сложные модели, такие как многоуровневая регрессия или нелинейные модели. Во-вторых, Excel может обрабатывать только ограниченное количество данных, что делает его неподходящим для больших наборов данных. В-третьих, интерпретация результатов требует определенных знаний статистики, так как Excel не предоставляет подробных объяснений. Для более сложных анализов рекомендуется использовать специализированные программы, такие как R или Python.