Корреляционный анализ в Excel: расчет и интерпретация связей данных

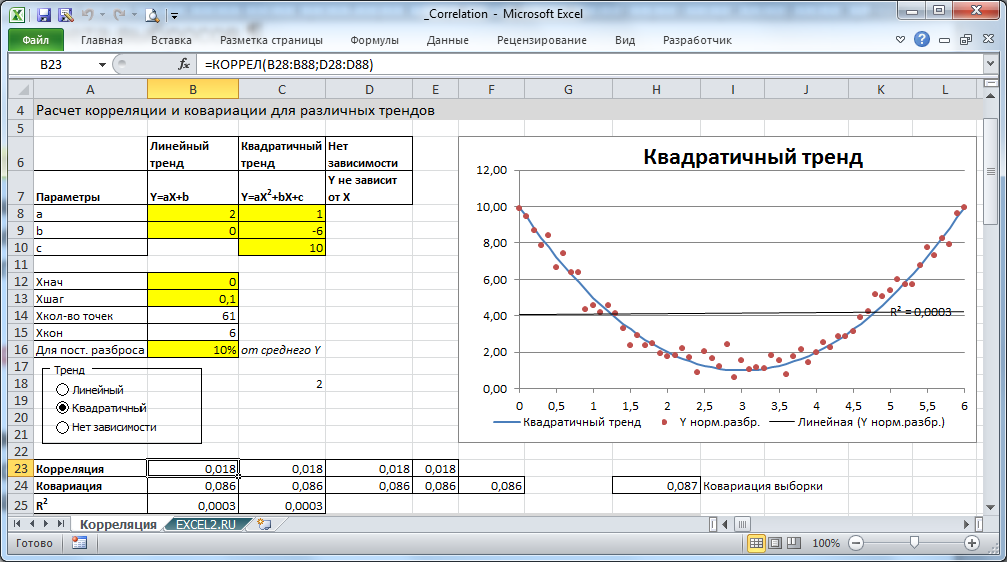
Корреляционный анализ — это статистический метод, который позволяет оценить силу и направление связи между двумя или более переменными. В этой статье мы рассмотрим, как проводить корреляционный анализ в Excel, используя встроенные функции и инструменты. Вы узнаете, как рассчитывать коэффициенты корреляции Пирсона и Спирмена, интерпретировать их значения и применять полученные результаты для анализа данных.

Мы также обсудим, как корреляция помогает выявлять закономерности в данных, что особенно полезно в таких областях, как экономика, маркетинг и финансы. Вы поймете, как использовать корреляционный анализ для прогнозирования и принятия обоснованных решений на основе данных. В конце статьи вы сможете самостоятельно применять эти методы для анализа взаимосвязей в своих данных.

Основные понятия корреляционного анализа

Корреляционный анализ — это статистический метод, используемый для изучения взаимосвязей между двумя или более переменными. Основная цель такого анализа — определить, существует ли зависимость между переменными и насколько она сильна. В Excel для этого используются коэффициенты корреляции, такие как коэффициент Пирсона и коэффициент Спирмена. Первый применяется для измерения линейной связи между переменными, а второй — для оценки монотонной связи, которая может быть нелинейной.

Коэффициент корреляции принимает значения от -1 до 1. Значение, близкое к 1, указывает на сильную положительную связь, когда увеличение одной переменной сопровождается увеличением другой. Значение, близкое к -1, свидетельствует о сильной отрицательной связи, при которой рост одной переменной приводит к уменьшению другой. Если коэффициент близок к 0, это говорит об отсутствии значимой связи между переменными.

Важно понимать, что корреляция не означает причинно-следственную связь. Даже если две переменные сильно коррелируют, это не обязательно означает, что одна из них вызывает изменения в другой. Для установления причинности требуются дополнительные исследования. Корреляционный анализ в Excel помогает выявить закономерности в данных, что делает его полезным инструментом в таких областях, как экономика, маркетинг и финансы.

Коэффициенты корреляции: Пирсон и Спирмен

Коэффициенты корреляции являются основным инструментом для измерения силы и направления связи между двумя переменными. В Excel чаще всего используются два типа коэффициентов: коэффициент корреляции Пирсона и коэффициент корреляции Спирмена.

Коэффициент Пирсона применяется для оценки линейной связи между переменными, которые имеют нормальное распределение. Он принимает значения от -1 до 1, где 1 указывает на полную прямую связь, -1 — на обратную, а 0 — на отсутствие связи. Этот метод идеально подходит для анализа данных, где важно понять, насколько изменения одной переменной влияют на другую.

Коэффициент Спирмена, в свою очередь, используется для оценки монотонной связи, которая не обязательно должна быть линейной. Он также варьируется от -1 до 1, но основывается на рангах данных, что делает его более устойчивым к выбросам и подходящим для данных с нестандартным распределением. Этот метод особенно полезен, когда данные содержат аномалии или не соответствуют предположениям о нормальности.

Оба коэффициента помогают выявить статистически значимые связи между переменными, но их выбор зависит от характера данных и целей анализа. Правильная интерпретация результатов позволяет сделать выводы о наличии или отсутствии зависимости, что является ключевым шагом для дальнейшего анализа и принятия решений.

Расчет корреляции в Excel с помощью функции CORREL

Корреляционный анализ — это мощный инструмент для изучения взаимосвязей между переменными. В Excel для расчета коэффициента корреляции чаще всего используется функция CORREL. Эта функция позволяет определить степень линейной зависимости между двумя наборами данных. Для ее использования достаточно указать два диапазона значений, между которыми необходимо вычислить корреляцию. Например, формула =CORREL(A2:A10, B2:B10) рассчитает коэффициент корреляции для данных в указанных диапазонах.

Результат функции CORREL варьируется от -1 до 1. Значение, близкое к 1, указывает на сильную положительную связь, то есть при увеличении одной переменной другая также возрастает. Значение, близкое к -1, свидетельствует о сильной отрицательной связи, когда увеличение одной переменной приводит к уменьшению другой. Если коэффициент близок к 0, это говорит об отсутствии линейной зависимости между переменными.

Важно помнить, что корреляция не означает причинно-следственную связь. Даже если две переменные демонстрируют высокий коэффициент корреляции, это не обязательно указывает на то, что одна из них влияет на другую. Поэтому интерпретация результатов должна быть осторожной и учитывать контекст данных.

Использование функции CORREL в Excel особенно полезно в таких областях, как экономика, маркетинг и финансы, где важно понимать взаимосвязи между различными показателями. Например, можно проанализировать, как изменения цен на товары влияют на объемы продаж, или как доходы компании связаны с уровнем инвестиций.

Таким образом, функция CORREL в Excel предоставляет простой и эффективный способ расчета корреляции, что делает ее незаменимым инструментом для анализа данных и принятия обоснованных решений.

Интерпретация результатов корреляционного анализа

Интерпретация результатов корреляционного анализа — это ключевой этап, который позволяет понять, насколько сильна и значима связь между переменными. Коэффициент корреляции может принимать значения от -1 до 1. Если значение близко к 1, это указывает на сильную положительную связь: при увеличении одной переменной другая также возрастает. Если коэффициент близок к -1, это свидетельствует о сильной отрицательной связи: рост одной переменной сопровождается снижением другой. Значение около 0 говорит об отсутствии линейной зависимости.

Важно учитывать уровень достоверности (p-value), который показывает, насколько статистически значимы полученные результаты. Обычно p-value менее 0,05 считается показателем значимой связи. Однако даже при высокой значимости следует помнить, что корреляция не означает причинно-следственную связь. Например, две переменные могут быть связаны из-за влияния третьего фактора.

Для более глубокого анализа рекомендуется визуализировать данные с помощью диаграмм рассеяния, которые помогают наглядно оценить характер связи. Также стоит учитывать контекст данных и возможные ограничения, такие как выбросы или нелинейные зависимости. Правильная интерпретация результатов позволяет использовать корреляционный анализ для прогнозирования, принятия решений и выявления скрытых закономерностей в данных.

Применение корреляционного анализа в различных областях

Корреляционный анализ является мощным инструментом для изучения взаимосвязей между переменными, который находит применение в самых разных сферах. В экономике он помогает выявить зависимости между показателями, такими как уровень инфляции и безработицы, что позволяет строить более точные прогнозы и разрабатывать эффективные стратегии. В маркетинге корреляционный анализ используется для определения связи между рекламными бюджетами и объемом продаж, что помогает оптимизировать расходы и повысить рентабельность кампаний.

В финансах этот метод позволяет анализировать взаимосвязи между курсами акций, процентными ставками и другими экономическими индикаторами. Это особенно важно для инвесторов, которые стремятся минимизировать риски и максимизировать доходность своих вложений. В научных исследованиях корреляционный анализ помогает установить связи между различными факторами, например, между уровнем загрязнения окружающей среды и заболеваемостью населения, что способствует разработке мер по улучшению экологической ситуации.

Таким образом, корреляционный анализ является универсальным инструментом, который помогает не только понять существующие взаимосвязи, но и использовать их для принятия обоснованных решений. Независимо от области применения, правильная интерпретация результатов анализа позволяет выявить скрытые закономерности и сделать данные более полезными для практического использования.

Заключение

Корреляционный анализ в Excel — это мощный инструмент для изучения взаимосвязей между переменными, который помогает выявить зависимости и закономерности в данных. В этой статье мы рассмотрели основные методы расчета корреляции, такие как использование функций CORREL и Пирсона, а также интерпретацию полученных результатов. Важно помнить, что корреляция не всегда означает причинно-следственную связь, и ее результаты требуют тщательного анализа.

Применение корреляционного анализа в экономике, маркетинге и финансах позволяет принимать обоснованные решения на основе данных. Например, выявление связи между спросом на продукт и его ценой может помочь в разработке эффективной стратегии ценообразования. Однако важно учитывать уровень достоверности и направление связи, чтобы избежать ошибочных выводов.

В заключение, корреляционный анализ в Excel — это не только инструмент для исследования данных, но и способ прогнозирования и оптимизации процессов. Используя его правильно, вы сможете глубже понять структуру данных и принимать более взвешенные решения.

Часто задаваемые вопросы

1. Что такое корреляционный анализ и зачем он нужен в Excel?

Корреляционный анализ — это статистический метод, который позволяет определить наличие и силу связи между двумя или более переменными. В Excel этот анализ используется для выявления зависимостей между данными, что помогает в прогнозировании, анализе тенденций и принятии решений. Например, с его помощью можно определить, как изменение одной переменной влияет на другую, что особенно полезно в экономике, маркетинге и научных исследованиях. Excel предоставляет удобные инструменты для расчета корреляции, такие как функция КОРРЕЛ и анализ данных через Пакет анализа.

2. Как рассчитать коэффициент корреляции в Excel?

Для расчета коэффициента корреляции в Excel можно использовать функцию КОРРЕЛ. Для этого необходимо выбрать два диапазона данных, между которыми нужно определить связь. Формула выглядит так: =КОРРЕЛ(диапазон1; диапазон2). Также можно воспользоваться Пакетом анализа, который доступен через вкладку "Данные". После активации пакета выберите опцию "Корреляция", укажите диапазон данных и настройте параметры. Коэффициент корреляции будет находиться в диапазоне от -1 до 1, где 1 означает сильную прямую связь, -1 — сильную обратную, а 0 — отсутствие связи.

3. Как интерпретировать результаты корреляционного анализа в Excel?

Интерпретация результатов корреляционного анализа зависит от значения коэффициента корреляции. Если коэффициент близок к 1, это указывает на сильную прямую связь: при увеличении одной переменной увеличивается и другая. Если коэффициент близок к -1, связь обратная: при увеличении одной переменной другая уменьшается. Значения около 0 говорят об отсутствии линейной связи. Однако важно помнить, что корреляция не означает причинно-следственную связь. Для более глубокого анализа рекомендуется использовать дополнительные методы, такие как регрессионный анализ.

4. Какие ограничения имеет корреляционный анализ в Excel?

Корреляционный анализ в Excel имеет несколько ограничений. Во-первых, он показывает только линейную связь между переменными, а нелинейные зависимости могут остаться незамеченными. Во-вторых, корреляция не доказывает причинно-следственную связь: даже если две переменные сильно коррелируют, это не означает, что одна вызывает другую. В-третьих, на результаты могут влиять выбросы в данных, что искажает коэффициент корреляции. Поэтому перед анализом важно очистить данные и проверить их на наличие аномалий.