Дисперсионный анализ в Excel: пошаговая инструкция с примерами

Дисперсионный анализ — это статистический метод, который позволяет сравнивать средние значения нескольких групп данных и определять, существуют ли статистически значимые различия между ними. В этой статье мы рассмотрим, как провести дисперсионный анализ в Excel, начиная с подготовки данных и заканчивая интерпретацией результатов. Вы узнаете, как использовать встроенные инструменты Excel для выполнения анализа, а также как правильно интерпретировать полученные результаты.

Мы также обсудим ключевые шаги, такие как выбор уровня значимости, анализ таблицы результатов и проверка предположений. Особое внимание будет уделено практическому применению дисперсионного анализа в различных областях, включая маркетинг, финансы и медицину. В конце статьи вы найдете примеры, которые помогут лучше понять, как использовать этот метод в реальных задачах.

Подготовка данных для дисперсионного анализа

Подготовка данных является важным этапом перед проведением дисперсионного анализа в Excel. На этом этапе необходимо убедиться, что данные структурированы и очищены от ошибок или пропущенных значений. Для этого рекомендуется проверить данные на наличие выбросов, которые могут исказить результаты анализа. Если такие значения обнаружены, их следует либо исключить, либо заменить на более репрезентативные.

Кроме того, данные должны быть группированы в соответствии с исследуемыми категориями. Например, если вы сравниваете эффективность нескольких маркетинговых стратегий, данные должны быть разделены на группы, соответствующие каждой стратегии. Это позволит корректно применить функцию АНАЛИЗ ВАРИАНТОВ в Excel.

Важно также убедиться, что данные соответствуют предположениям дисперсионного анализа, таким как нормальность распределения и однородность дисперсий. Для проверки этих условий можно использовать дополнительные инструменты Excel, например, построение гистограмм или тесты на нормальность. Только после тщательной подготовки данных можно переходить к следующему этапу — проведению самого анализа.

Использование функции АНАЛИЗ ВАРИАНТОВ

Функция АНАЛИЗ ВАРИАНТОВ в Excel является мощным инструментом для проведения дисперсионного анализа, который позволяет сравнивать средние значения нескольких групп данных. Эта функция особенно полезна, когда необходимо определить, существуют ли статистически значимые различия между группами. Для начала работы с функцией необходимо убедиться, что данные подготовлены: они должны быть очищены от ошибок и корректно сгруппированы.

После подготовки данных можно перейти к настройке параметров анализа. В Excel функция АНАЛИЗ ВАРИАНТОВ доступна через меню "Данные" в разделе "Анализ данных". Здесь важно выбрать правильную модель анализа, например, однофакторный или двухфакторный дисперсионный анализ, в зависимости от структуры данных. После выбора модели необходимо указать диапазон данных и уровень значимости, который обычно устанавливается на уровне 0,05.

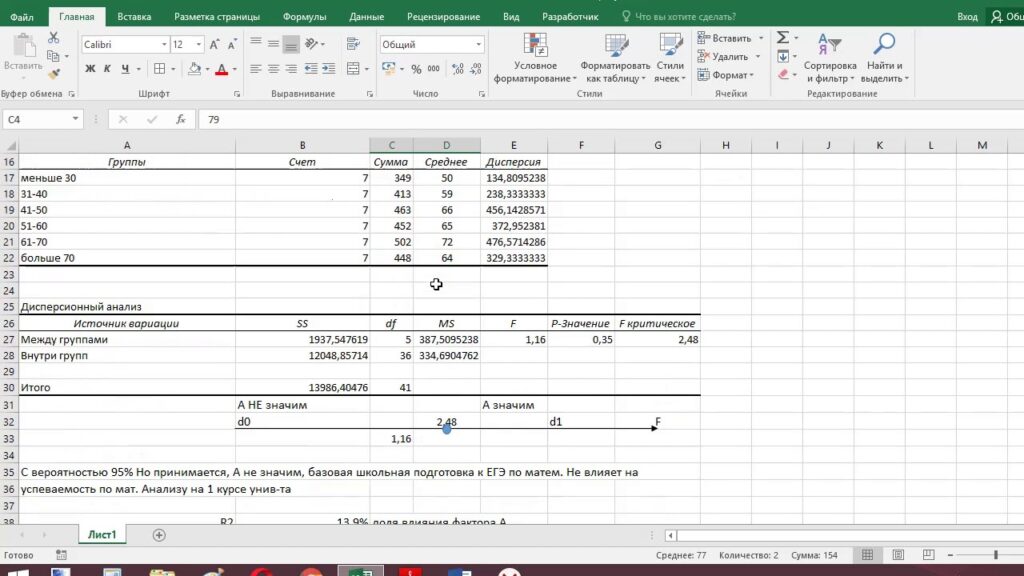
Результаты анализа выводятся в виде таблицы, где ключевыми показателями являются F-статистика и p-значение. Эти показатели помогают определить, есть ли статистически значимые различия между группами. Если p-значение меньше уровня значимости, можно сделать вывод о наличии таких различий. Интерпретация результатов требует внимательного анализа, так как важно учитывать не только статистическую значимость, но и практическую применимость полученных данных.

Использование функции АНАЛИЗ ВАРИАНТОВ в Excel позволяет эффективно решать задачи в различных областях, таких как маркетинг, финансы и медицина. Однако важно помнить, что корректность результатов зависит от соблюдения предположений дисперсионного анализа, таких как нормальность распределения данных и однородность дисперсий. В случае нарушения этих условий может потребоваться применение альтернативных методов анализа.

Выбор уровня значимости и анализ таблицы результатов

Выбор уровня значимости является важным этапом при проведении дисперсионного анализа. Уровень значимости, обозначаемый как α, определяет вероятность ошибки первого рода, то есть вероятность отвергнуть нулевую гипотезу, когда она на самом деле верна. Обычно используется значение α = 0,05, что соответствует 5%-ному уровню значимости. Однако в зависимости от задачи и требований к точности анализа этот параметр может быть изменён. Например, в медицинских исследованиях часто применяют более строгий уровень значимости, например α = 0,01, чтобы минимизировать вероятность ложных выводов.

После выбора уровня значимости важно правильно интерпретировать результаты, представленные в таблице дисперсионного анализа. Основное внимание следует уделить значению p-value, которое указывает на вероятность получения наблюдаемых различий между группами при условии, что нулевая гипотеза верна. Если p-value меньше выбранного уровня значимости, это свидетельствует о наличии статистически значимых различий между группами. В противном случае различия считаются незначимыми.

Кроме p-value, в таблице результатов представлены такие показатели, как сумма квадратов, степени свободы и F-статистика. Сумма квадратов отражает общую вариацию данных, разделённую на вариацию между группами и внутри групп. F-статистика позволяет оценить, насколько различия между группами превышают случайные колебания внутри групп. Чем выше значение F-статистики, тем больше вероятность того, что различия между группами не случайны.

Интерпретация результатов должна быть основана не только на числовых значениях, но и на контексте исследования. Например, даже если p-value указывает на статистическую значимость, важно учитывать практическую значимость различий. В некоторых случаях небольшие различия могут быть статистически значимыми, но не иметь реального значения для практического применения. Поэтому анализ таблицы результатов должен быть комплексным и учитывать как статистические, так и содержательные аспекты исследования.

Интерпретация результатов и построение графиков

После проведения дисперсионного анализа в Excel важно правильно интерпретировать полученные результаты. Основное внимание следует уделить таблице, которая содержит ключевые показатели, такие как F-статистика, p-значение и суммы квадратов. F-статистика позволяет определить, есть ли статистически значимые различия между средними значениями групп. Если p-значение меньше выбранного уровня значимости (обычно 0,05), это свидетельствует о наличии значимых различий.

Для визуализации результатов рекомендуется построить графики, которые помогут наглядно представить различия между группами. Например, можно использовать столбчатые диаграммы или линейные графики, чтобы отобразить средние значения и их доверительные интервалы. Это особенно полезно при презентации данных, так как графики делают информацию более доступной для восприятия.

Кроме того, важно провести анализ остатков, чтобы убедиться в корректности модели. Остатки должны быть случайно распределены вокруг нуля, что можно проверить с помощью графика остатков. Если на графике видны закономерности, это может указывать на нарушение предположений модели, таких как гомогенность дисперсий или нормальность распределения. В таком случае может потребоваться корректировка данных или выбор другой модели анализа.

Интерпретация результатов и построение графиков завершают процесс дисперсионного анализа, позволяя сделать выводы и принять обоснованные решения на основе данных.

Практическое применение дисперсионного анализа

Дисперсионный анализ (ANOVA) — это мощный статистический инструмент, который позволяет сравнивать средние значения нескольких групп данных. Он широко применяется в различных областях, таких как маркетинг, финансы, медицина и научные исследования. Например, в маркетинге дисперсионный анализ помогает определить, влияет ли изменение цены на уровень продаж. В медицине его используют для сравнения эффективности различных методов лечения. В финансах ANOVA может помочь выявить различия в доходности инвестиционных портфелей.

Одним из ключевых преимуществ дисперсионного анализа является его способность одновременно сравнивать несколько групп, что делает его более эффективным по сравнению с множественными t-тестами. Это особенно полезно, когда необходимо проанализировать влияние нескольких факторов на исследуемую переменную. Например, в производственной сфере можно оценить, как различные комбинации сырья и технологий влияют на качество продукции.

Интерпретация результатов дисперсионного анализа требует внимательного подхода. Важно учитывать не только уровень значимости (p-value), но и эффект взаимодействия между факторами. Это позволяет сделать более точные выводы и принять обоснованные решения. Например, если анализ показывает значимые различия между группами, это может стать основанием для изменения стратегии или внедрения новых методов работы.

Заключение

Заключение

Дисперсионный анализ в Excel — это мощный инструмент для сравнения средних значений между группами данных и выявления статистически значимых различий. В статье мы рассмотрели основные шаги, начиная с подготовки данных и заканчивая интерпретацией результатов. Функция АНАЛИЗ ВАРИАНТОВ позволяет эффективно проводить анализ, а правильный выбор уровня значимости и модели обеспечивает точность выводов.

Важно помнить, что успешное применение дисперсионного анализа требует соблюдения ключевых предположений, таких как нормальность распределения данных и однородность дисперсий. Если эти условия не выполняются, результаты могут быть искажены. Кроме того, анализ остатков помогает выявить возможные ошибки и улучшить качество модели.

Дисперсионный анализ находит применение в различных областях, включая маркетинг, финансы и медицину, где требуется сравнение групп и выявление факторов, влияющих на результат. Использование Excel делает этот метод доступным даже для пользователей без глубоких знаний в статистике, но важно подходить к анализу с пониманием его ограничений и особенностей.

В заключение, дисперсионный анализ в Excel — это не только инструмент для обработки данных, но и способ сделать обоснованные выводы, которые могут повлиять на принятие решений в бизнесе и науке.

Часто задаваемые вопросы

1. Что такое дисперсионный анализ и зачем он используется в Excel?

Дисперсионный анализ (ANOVA) — это статистический метод, который позволяет сравнивать средние значения нескольких групп данных и определять, есть ли между ними статистически значимые различия. В Excel этот метод используется для анализа данных, например, в маркетинговых исследованиях, научных экспериментах или управлении качеством. Основная цель — выяснить, влияет ли какой-либо фактор (например, тип рекламы или метод производства) на результат (например, продажи или качество продукции). Excel предоставляет удобные инструменты для выполнения дисперсионного анализа, такие как надстройка "Анализ данных", которая упрощает процесс.

2. Как подготовить данные для дисперсионного анализа в Excel?

Для выполнения дисперсионного анализа данные должны быть организованы в табличном формате. Каждая группа данных должна располагаться в отдельном столбце или строке. Например, если вы сравниваете результаты трех разных методов обучения, то данные по каждому методу должны быть в своем столбце. Важно, чтобы данные были числовыми и не содержали пропусков или ошибок. Перед анализом рекомендуется проверить данные на нормальность распределения и гомогенность дисперсий, чтобы убедиться в корректности применения метода.

3. Как выполнить дисперсионный анализ в Excel?

Для выполнения дисперсионного анализа в Excel необходимо:
1. Включить надстройку "Анализ данных" через меню "Файл" -> "Параметры" -> "Надстройки".
2. Выбрать инструмент "Однофакторный дисперсионный анализ" в разделе "Анализ данных".
3. Указать диапазон данных и параметры анализа, такие как уровень значимости (обычно 0,05).
4. Нажать "ОК" и проанализировать результаты. Основные показатели, на которые стоит обратить внимание, — это F-статистика и p-значение. Если p-значение меньше уровня значимости, это означает, что между группами есть статистически значимые различия.

4. Как интерпретировать результаты дисперсионного анализа в Excel?

Результаты дисперсионного анализа в Excel включают несколько ключевых показателей. F-статистика показывает соотношение между дисперсией внутри групп и дисперсией между группами. Чем выше значение F, тем больше вероятность, что различия между группами значимы. P-значение указывает на вероятность того, что различия случайны. Если p-значение меньше выбранного уровня значимости (например, 0,05), можно сделать вывод о наличии статистически значимых различий. Также в результатах отображаются средние значения для каждой группы, что помогает понять, в какую сторону направлены различия.